List of Figures

• Structure of C₈K, a typical stage 1 intercalation compound. Stage n means that n layers of graphite are present between each pair of intercalant layers.[67] a) The layer structure. The lattice constant along the direction perpendicular to the planes is called I_c in GIC's. b) Three common in-plane structures. C₈K has the (2 × 2)R0° structure.
• Evidence for dimensionality crossover in a Nb/Ge superlattice.[208] Solid lines are fits to the KLB theory.[131] The direction marked ``||'' means _|_ ^c in the vernacular of GIC's and the direction marked ``_|_'' is || ^c in GIC terms. The H_c2 data marked _|_ is almost unaffected by the dimensionality crossover. The H_c2 data marked || covers the range from the fully 3D regime (45 Å/ 7 Å specimen) to the fully 2D regime (45 Å/ 50 Å specimen). The intermediate 65 Å/35 Å specimen shows a crossover from 3D to 2D character as the temperature is lowered.
• H_c2(t) data on Nb/Ta superlattices showing two low-temperature critical field discontinuities. From Ref. [30]. The discontinuity in slope at t 0.8-0.9 is the 3D-2D coupling change. The identity of the lower transition at t = 0.49 has not been definitely determined.
• H_c2(theta) data on Nb/Ta superlattices from Ref. [29]. The data is for three samples at a reduced temperature t = 0.9. Lambda is the bilayer period, which corresponds to I_c in the GIC case. Data in the trace marked 3D are fit 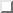with Eqn. , while data in the traces marked 2D are fit with Eqn. .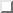
• T_c vs layer thickness in Nb/Cu superlattices. From Ref. [14]. The decrease of T_c with decreasing thickness of the superconducting component is predicted by proximity-effect theories.[49,54] The predictions of the standard proximity-effect theories is indicated by the solid line. The proximity effect calculation modified to allow a thickness-dependent T_c for the Nb layers is indicated by the dashed line.
• H_c2(theta) for a high- T_c superconductor. From Ref. [118]. Each set of symbols corresponds to a different definition of H_c2. For example, the curve labeled 0.7 R _N was obtained by plotting versus theta the values of H that satisfy R(H,theta) = 0.7 R_N. Each curve is also labeled in parentheses with the magnitude of the anisotropy parameter 1/epsilon that was used for the fit to Eqn. .
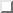• Phase diagrams of the K-Hg and Cs-Bi binary alloys.[103]
• Range of compositions of the starting alloy which will produce a given stage GIC in the K-Hg and Cs-Bi binary systems. From Ref. [145]. Upper, K-Hg system. In region (1), C₈K is produced; in region (2), C₄KHg; in region (3), C₈KHg; in region (4), C₁₂KHg; in region (5), higher-stage binary compounds, or no reaction. Lower, Cs-Bi system. In region (1), C₈Cs is produced; in (2), C₄CsBi; in region (3), no reaction.
• (00l) x-ray scans for pink and gold C₄KHg. The large peak near 22° in each scan is from the copper sample holder. The broad hump from about 6° to 14° is due to the glass tube that the sample holder is in. a) I_c = (10.22 ± 0.03) Å pink sample. T_c = 1.53 K. b) I_c = (10.18 ± 0.03) Å gold sample. T_c = 0.95 K.
• (00l) x-ray scans before and after hydrogenation for a gold C₄KHg sample. The broad hump from about 6° to 14° is due to the glass tube that the sample is in. Before: T_c = 0.84 K gold C₄KHg sample. I_c = (10.24 ± 0.03) Å. After: Same sample as in ``Before'' picture, only after exposure to 200 torr hydrogen gas. T_c = 1.535 K. I_c = (10.24 ± 0.03) Å.
• (00l) x-ray scans for alpha-phase stage 1 CsBi-GIC's. The broad hump from about 6° to 14° is due to the glass tube that the sample holder is in. a) I_c = (10.61 ± 0.03) Å alpha-phase sample. b) Similar (00l) scan taken by Bendriss-Rerhrhaye.[17] In b), theta is increasing from right to left, whereas in a) 2theta is increasing from left to right.
• Raman spectra on gold and pink C₄KHg. a) Spectrum of a T_c = 0.719 K gold sample with a single I_c value = 10.14 Å. The peak frequency is 1597.1 cm^-1 and the HWHM is 13.2 cm^-1. b) Spectrum of a T_c = 1.53 K pink sample with a single I_c value = 10.22 Å. The peak frequency is 1593.9 cm^-1 and the HWHM is 15.5 cm^-1.
• X-ray and neutron diffraction (00l) spectra of a gold C₄KHg specimen. The beta-phase peaks are marked with downarrow. a) Only the I_c = 10.24 Å alpha phase is clearly visible using x-rays. The small bump to the left of the (002) may be the beta-phase (002) peak. b) With neutrons, both the I_c = 10.24 Å alpha phase and the I_c = 10.83 Å beta phase show well-defined peaks.
• Neutron diffraction spectra of a gold C₄KHg specimen with hydrogen and a pink specimen without hydrogen. Note the lack of beta phase in either sample. a) Spectrum of a gold sample whose T_c was 0.84 K before hydrogenation and 1.54 K afterward. b) Spectrum of a pink C₄KHg sample.
• Definition of the distances z_i used in the fits to the neutron diffraction data (from Ref. [272]). The distances are measured from the center of the sandwich, halfway between the mercury layers. Deltaz, the Hg layer splitting, is twice the distance of the Hg layers from z = 0.
• Real-space structure of the majority phase of C₄KHg along the c-axis as calculated from the Fourier transform of the extended neutron diffraction data. All plots were scaled to a carbon peak height of 1.0. a) Plot of nuclear scattering intensity versus distance along the graphite c-axis for a pink sample (*) and a gold sample (circ). b) A similar plot comparing the structure of the MIT pink sample (*) to a structure (circ) calculated from fit parameters reported by Yang et al.[272]
• Experimental definition of T_c.
• a) dc magnetization versus field for ideal type I and type II superconductors. H_c1 is the lower critical field, H_c is the thermodynamic critical field, and H_c2 is the upper critical field. kappa < 1/sqrt2 indicates type I superconductivity; kappa 0.8 indicates weak type II behavior; kappa 2 indicates strongly type II behavior. b) ac susceptibility versus field for ideal type II superconductor with kappa 0.8. Adapted from Ref. [252].
• A sketch of the sample holder used in the critical field measurements. The dimension d of the metal piece was chosen to be the inner diameter of the sample tube so that the holder would be centered and fixed inside the tube. A careful effort was made to orient the carbon (graphene) planes parallel to the holder's surface. The GIC's were affixed to the metal pieces with Apiezon N grease.
• A schematic drawing of the inductance bridge. The sample capsule was placed inside the primary coil. The windings were made from 38 gauge magnet wire. There were 20 complete layers of winding in the secondary coils and 2 complete layers of winding in the primary.
• A schematic of the data acquisition system. For zero-field temperature sweeps, the thermometer voltage was attached to the x-input of the flatbed plotter. For fixed-temperature magnetic field sweeps, the dc output of a stepping motor on the magnet power supply was attached to the x-input of the plotter.
• Illustration of how a sample which is only partially superconducting can mimic full superconductivity in an inductive transition.
• a) Definition of the angle theta, the angle between the applied magnetic field and the graphite c-axis. This angle is the complement to that usually used in the thin-film superconductivity literature, but corresponds to customary usage in the GIC literature. b) A sketch showing how H_c2 is determined graphically from raw susceptibility versus magnetic field data. Note the similarity of this trace to Figure b).
• a) Superconducting transitions with the magnetic field applied parallel and perpendicular to the graphite c-axis for a typical C₄KHg sample. Notice how much broader the transition is in the vecH_|_ ^c case. b) Similar data from Iye and Tanuma, Ref.[120], Figure 2.
• Critical field H_c2 as a function of the angle theta for 4 C₄KHg GIC's at T 0.4 K. Fits (dotted lines) were calculated using Equation . a) Data for an MIT C₄KHg sample with T_c = 0.95 K (circ) and also for a T_c = 0.73 K sample (bullet) from Ref. [240]. For T_c = 0.95 K sample, 1/epsilon = 10.0 and H_c2(0°) = 24 Oe with a residual cal R = 0.29. For data of Ref. [240], 1/epsilon = 11.3, H_c2(0°) = 26 Oe, and cal R = 0.090. b) Data for two C₄KHg samples with T_c 1.5 K. (circ), T_c = 1.53 K with 1/epsilon = 10.2, H_c2(0°) = 46 Oe, and cal R = 0.73; bullet, T_c = 1.54 K with 1/epsilon = 9.5, H_c2(0°) = 47 Oe, and cal R = 1.18.
• Why a tilted sample affects the shape of H_c2(theta). The notation ( vecH cdot ^x)^x signifies the projection of vecH along ^x. a) The aligned case. Rotations of the sample around the vertical ^z allow theta to be varied all the way from ( vecH||^c) to ( vecH_|_^c) ( vecH_|_^c = vecH|| ^a). b) The misaligned case. H_{c2,_|_^c} can still be measured correctly, but instead of the true value of H_c2||^c one will get H_c2,||^c/sqrtcos²ø + epsilon²sin²ø.
• The effect of sample tilt on H_c2(theta). The three curves in this picture were calculated using the parameters H_{c2,|| ^c} = 42 Oe, anisotropy == 1/epsilon = 15 and the following values for the tilt angle: (circ) ø = 0°; (bullet) ø = 10°; (diamond) ø = 40°. The ø = 0° curve corresponds to one of the fits shown in Figure b). Note that the curves for ø = 10° and for ø = 0° are almost indistinguishable.
• The effect of mosaic spread on H_c2(theta), calculated using Equation . The same parameters were used as in Figure , except that here the mosaic spread, Delta, is varied: (circ) Delta = 0°; (bullet) Delta = 3°; (diamond) Delta = 10°.
• Comparison of the effect of the two definitions of H_c2 on H_c2(theta). circ, tangent definition; diamond, 90% definition. Data are for a T_c = 1.53 K sample at T/T _c = 0.29. The 90% method tends to produce slightly higher critical fields, but there is only a small difference between the shapes of the curves for the two analysis methods. Use of the 90% definition does not improve agreement with Eqn. .
• H_c2(theta) for C₈K, from Ref. [141]. The fields are labeled H_c2 in the type II region and H_c3 and H_c in the type I region.
• H_c2(theta) curves for TaN showing a transition from type I to type II character as a function of field direction. From Ref. [259]. TaN is the only bulk superconductor besides C₈K (and possibly C₄KHg) known to display this variability. The temperatures at which the curves were taken and the thermodynamic critical fields are indicated. Note that at 1.65 K, the sample is entirely type II, but that at 2.4 K it is entirely type I.
• Anisotropic Ginzburg-Landau model fits (dotted curves) to H_c2(theta) data as a function of temperature. All fits were produced with the parameters tilt = 0° and mosaic spread = 0°. a) t = 0.29, H_c2,||^c = 47 Oe, anisotropy (1/epsilon) = 9.5, and residual parameter cal R = 1.18. b) t = 0.57, H_{c2, ||^c} = 33 Oe, anisotropy (1/epsilon) = 5.5, and cal R = 1.25. c) t = 0.78, H_c2,||^c = 23.1 Oe, anisotropy (1/epsilon) = 4.5, and cal R = 1.43.
• Anisotropic Ginzburg-Landau model fits (dotted curves) to H_c2(theta) data as a function of temperature, taking into account the possibility of type I behavior. All fits were produced with the parameters tilt = 0° and mosaic spread = 0°. a) t = 0.29, H_c2,||^c = 35 Oe, anisotropy (1/epsilon) = 14, H_c = 65 Oe, and residual parameter cal R = 0.39. b) t = 0.57, H_{c2, ||^c} = 19 Oe, anisotropy (1/epsilon) = 15.5, H_c = 43 Oe, and cal R = 0.84. c) t = 0.78, H_c2,||^c = 14.5 Oe, anisotropy (1/ epsilon) = 12.5, H_c = 24.5 Oe, and cal R = 1.11.
• Comparison of field sweeps between type II and possible type I transitions. The vertical direction is the inductive voltage, while the horizontal direction is field. All traces taken at about 0.4 K. a) Transitions with vecH _|_ ^c and vecH || ^c for a T_c = 0.95 K sample. For both orientations the transitions appear smooth. b) Transitions with vecH _|_ ^c and vecH || ^c for a T_c = 1.5 K sample. For vecH _|_ ^c, the transition looks smooth, consistent with its expected type II character. For vecH || ^c, on the other hand, there is a small discontinuity in the susceptibility near the upper critical field which is indicated by an arrow. This feature was seen consistently in T_c = 1.5 K samples.
• Thermodynamic critical fields obtained from H_c2(theta) fits versus temperature for T_c = 1.5 K C₄KHg specimens. The numbers plotted here are the same as in Table . (bigtriangleup), data for a T_c = 1.53 K sample; (circ), data for a T_c = 1.54 K sample; (diamond), a linear fit to the data with H_c(0) = 85.2 g; (circ), a quadratic fit to the data with H_c(0) = 66.5 g; (×), H_c(t) calculated using the specific heat data of Alexander et al.,[8] which gives H_c(0) = 112 Oe.
• Comparison of the Tinkham formula and AGL theory fits to H_c2(theta) data on a T_c = 1.5 K C₄KHg-GIC. bullet, data at t = 0.55. circ, AGL fit with H_c2(0°) = 19 Oe, 1/epsilon = 15.5, and a residual cal R = 0.84. diamond, TF fit with H_c2(0°) = 23 Oe, 1/epsilon = 13, H_c = 41 Oe, and cal R = 0.47. Below, a plot of the errors of each fit versus theta. The same symbols are used.
• Critical field H_c2 as a function of reduced temperature for C₄KHg. Dotted curves are least-squares line fits to the data. Fit parameters are given in Table . a) Data for a C₄KHg with T_c = 0.95 K: (circ), vecH _|_ ^c. (bullet), vecH || ^c Data for a T_c = 0.73 K sample from Ref. [240]: (diamond), vecH _|_ ^c. (×), vecH || ^c. b) Data for two C₄KHg-GIC's with T_c 1.5 K. T_c = 1.53 K sample: (circ), vecH _|_ ^c. (bullet), vecH || ^c. T_c = 1.54 K sample: diamond, vecH _|_ ^c. ×, vecH || ^c.
• Critical fields with vecH || ^c for T_c 1.5 K C₄KHg samples. Uparrow marks the value of T_c found using a zero-field temperature sweep. a) (bullet), data for a T_c = 1.53 K sample; (diamond), a linear fit to the data with H_c2(0) = 89.7 Oe, T_c = 1.65 K and cal R = 6.25e-3; (.), a quadratic fit to the data with H_c2(0) = 64.0 Oe, T_c = 1.55 K and cal R = 1.2e-2. b) (bullet), data for a T_c = 1.54 K sample; (diamond), a linear fit to the data with H_c2(0) = 85.8 Oe, T_c = 1.62 K and cal R = 1.62e-3; (.), a quadratic fit to the data with H_c2(0) = 62.8 Oe, T_c = 1.51 K and cal R = 4.7e-2.
• Comparison of WHH and linear fits to H_c2(T) data taken on a T_c = 1.54 K sample. a) (bullet), data for vecH _|_ ^c. (.), linear fit with H_c2(0) = 748 Oe, T_c = 1.52 K, and cal R = 6.9e-3. (circ), WHH fit with H_c2(0) = 518 Oe, T_c = 1.53 K, and cal R = 1.6e-2. b) (bullet), data with vecH || ^c. (.), linear fit with H_c2(0) = 85.8 Oe, T_c = 1.62 K, and cal R = 1.6e-3. (circ), WHH fit with H_c2(0) = 59.76 Oe, T_c = 1.63 K, and cal R = 1.2e-2.
• Summary of all H_c2 data, both _|_ and || to the c-axis. The dimensionless quantities plotted are reduced field ( h^*) versus reduced temperature (t). (bullet), 143 data points taken on 5 different GIC's. (circ), best 2-parameter WHH fit to the data with cal R = 1.7e-2. (.), best linear fit to the data with cal R = 1.3e-2. Both fits have fracdh^*dt = -1 at t = 1.
• Demonstration of the temperature dependence of the anisotropy parameter epsilon in C₄KHg, where 1/epsilon == H_c2(90°)/H_c2(0°). Data are for a T_c = 1.54 K C₄KHg sample. (circ), t = 0.29. (bullet), t = 0.55. (×), t = 0.76. All H_c2(0°) values were determined from the data, not the fits, so that this plot is model-independent. Fits to this data are shown in Figure .
• Temperature-dependent anisotropy in C₈KHg is demonstrated by a plot of H_c2(theta)/H_c2(0°) versus theta, just as in Figure . All data from Iye and Tanuma, Ref. [240] on a T_c = 1.94 K sample. (×), data at t = 0.23. Fit, (diamond), with 1/epsilon = 17.6 and cal R = 6.8e-3. (bullet), data at t = 0.81. (circ), fit with 1/epsilon = 21.6 and cal R = 5.3e-3.
• Positive curvature of H_c2(T) in C₈RbHg. Data are taken from Iye and Tanuma, Ref. [120]. (circ), H_{c2, _|_ ^c}. (bullet), H_{c2, || ^c}. Parameters for the line fits: for vecH _|_ ^c, H_c2(0) = 3078 Oe, T_c = 1.36 K, and cal R = 0.56; for vecH || ^c, H_c2(0) = 89.0 Oe, T_c = 1.37 K, and cal R = 3.02e-2. Zero-field T_c for this sample was 1.4 K.[120]
• Theoretical demonstration of dimensional crossover in Josephson-coupled superlattices from the work of Klemm, Luther and Beasley.[131]. r is the parameter which characterizes the dimensionality of coupling. alpha, tau_SO, and H _P == 4 k_B T_c/ pi mu are parameters which characterize the degree of Pauli-limiting (Pauli-limiting is discussed in Section ). The inset shows a plot of T^*/ T_c (where T^* is the dimensionality crossover temperature) versus r.
• T_c versus normal-layer thickness for S/N bilayers. Figure taken from Ref. [261] Here D _N and D _S are the thicknesses of the normal and superconducting layers, and T _cS is the bulk T_c of the superconducting component. Approximately T/ T_cS = (1 - t(D_N -> infty))(1 - exp-2D_N/xi), where xi is the dirty-limit Pippard coherence length.
• Extended critical field linearity due to small-scale sample inhomogeneity. From a calculation by Carter and colleagues.[34] The plots are of reduced field versus reduced temperature for several different normalized diffusivity distribution functions Q(y). Q(y) == D_aveP(D), where P(D) is the distribution function for diffusivity, D_ave is the average diffusivity, and y == D/D _ave. In the lower plot, a P(D) skewed to lower diffusivities produces an even greater critical field enhancement at low temperatures. The index n refers to the power of the linear factor used to skew the symmetric distribution.
• Illustration of how v_{_|_ vecH} (vecq) changes as a function of wavevector vecq for an ellipsoidal Fermi surface. vecq is the coordinate of a point on the Fermi surface. B is Dalrymple's anisotropy parameter, which is equivalent to epsilon in the AGL model.[50]
• Enhanced linearity of h^*(t) calculated from Butler's equations[33] using an ellipsoidal FS model. Taken from Ref. [50]. Dalrymple's parameter B is equivalent to 1/epsilon in the AGL model. The B = 1.0 curve is for a spherical Fermi Surface, and so is equivalent to the WHH theory.
• Butler-model[33] fit of NbSe₂ H_c2(t) data. Figures taken from Dalrymple's thesis.[50] a) H_{c2, _|_} = H_{c2, || ^c}. An excellent fit is obtained by using the Wexler-Woolley Fermi Surface model[263] plus an additional ellipsoid. b) H_{c2, ||} = H_{c2, _|_ ^c}. The Wexler-Woolley-plus-ellipsoid model produces the correct shape, but needs to be multiplied by an additional factor of 2.1 to account for mean-free-path anisotropy.
• Two-band model fit to anomalous H_c2(t) of Cs_0.1WO_2.9F_0.1 from Ref. [81]. The plot is of h^* versus t. The curve labeled (4) is the Helfand-Werthamer isotropic theory. The crosses, circles and squares are experimental data for three different crystallographic orientations (the orientations are not specified). Curve (1) is the two-band model with no interband-scattering, whereas (2) and (3) correspond to increasing interband-scattering. The parameters of these fits are too numerous to list here, but may be found in Ref. [81].
• Fermi surface computed for C₄KHg by Holzwarth and colleagues.[112] The basic structure of the Fermi surface is similar to that of NbSe₂[51] in that both have pieces of nearly cylindrical symmetry at the corner of a hexagonal Brillouin zone, and both have higher masses for transport along k_z than in the layer planes. The hexagonal solid line is the Brillouin zone; the roughly triangular pieces drawn with a solid line at the corners of the BZ are the graphitic pi bands. The pieces drawn with a dotted line are due to mercury bands. The small circular zone-center part is from Hg 6s holes; the hexagonal portion is from Hg 6ppi electron carriers; and the trigonal pieces at the zone corner are derived from H 6psigma bands.
• Comparison of H_c2(T) in C₈K and C₆K, one of its high-pressure phases. a) Data on a T_c = 134 mK C₈K sample taken by Koike and Tanuma.[141] Note the marked positive curvature of the critical fields. H_sc|| is a supercooling field. b) Data on a T_c = 1.5 K sample of C₆K from Ref. [13]. (circ), H_{c2, _|_ ^c}; (bigtriangleup), H_{c2, || ^c}. Note the enhanced linearity of the critical fields.
• Hydrogen stoichiometry dependence of the superconducting transition temperature T_c, Debye temperature theta_D, the Einstein temperature T_E, and the linear specific heat coefficient Gamma in C₈KH_x and C₈RbH_x. From Ref. [78]. The label F(x)/F(0) indicates that each of the quantities is plotted normalized to 1.0 at x = 0.
• Schematic density-of-states for a) C₈K and b) C₈KH_0.55. From Ref. [171]. Note the very small hole band near E_F in b).
• T_c increase in TaS₂ induced by a) hydrogenation and b) pressure. a) From Ref. [179]. The error bars represent the transition width, while the circles are the volume % superconducting. This experiment was performed on a powder sample. At a hydrogen concentration ofu.87, T_c ;SPM_lt; 0.5 K (not shown). b) From Ref. [90]. T_CDW is the CDW onset temperature, while T_c is the usual superconducting transition temperature. 4H _b and 2H are TaS₂ polytypes with different crystal structures.
• In-plane resistivity discontinuities in TaSe₂ associated with CDW formation. From Ref. [264]. 1T- and 2H- refer to different polytypes (crystal structures). The CDW transitions occur at 473 K in 1T-TaSe₂ and at 117 K in 2H-TaSe₂, respectively. Notice that 1T-TaSe₂ has a higher resistivity below its transition, whereas the resistivity of 2H-TaSe₂ decreases at its transition.
• Superconducting transitions before and after hydrogenation in three types of C₄KHg samples. a) A gold sample. T_c increases from 0.88 K to 1.54 K, and Delta T_c/ T_c decreases from 7.3× 10^-2 to 7.8× 10^-2. b) A pink sample. T_c is almost constant; Delta T_c/ T_c decreases from 4.7× 10^-2 to 2.2× 10^-2. c) A copper-colored sample. T_c increase from 1.32 K to 1.50 K; Delta T_c/ T_c decreases from 0.138 to 6.47× 10^-2.
• Pressure dependence of T_c in KHg-GIC's. From Ref. [55]. a) Pressure-induced transition narrowing in C₄KHg. Notice that the application of a small pressure, 0.8 kbar, increases T_c to 1.5 K, while application of further pressure decreases T_c at a rate dT_c/dP = -5×10^-5 K/bar. b) Monotonic decline of T_c with pressure in C₈KHg. dT_c/dP = -6.5×10^-5 K/bar.
• Possible Fermi surface nesting wave vector in C₈K. From Ref. [115]. The horizontal cross-section of the FS in the Gamma-K-M plane is shown. The arrow indicates the proposed nesting wave vector near the M point.
• Temperature dependence of the resistivity and susceptibility in the alkali-metal mercury GIC's. From Ref. [72]. a) Temperature dependence of the resisitivity. Curves (1) and (2) are for C₄RbHg; (3) is for C₄KHg; (4) is for C₈RbHg; and (5) is for C₈KHg. b) Temperature dependence of the susceptibility. Curves (1) and (2) are for C₄KHg; (3) is for C₈RbHg; (4) is for C₄K_0.5Rb_0.5Hg; (5) is for C₄RbHg, and (6) is for C₈KHg.
• An electron micrograph showing intercalant inclusions (bright regions) in a C₄CsBi_x alpha + beta-phase polycrystal grown here at MIT. The magnification for this micrograph is indicated by the 100 nm scale bar. [Micrograph prepared by J. Speck, MIT.]
• A plot of superconducting transition temperature T_c for C₄CsBi_x versus starting alloy Bi/Cs ratio. bigotimes, MIT data from Ref. [36]; bigtriangleup, University of Kentucky data from Ref. [270]; and bigcirc, Freie Universität Berlin data from Ref. [223]. The X are alloy (not GIC) data from the CRC Handbook. The presence of downarrow means that the nearest point represents an upper bound on T_c. Data from the University of Nancy is not included because precise starting alloy compositions are not given for their samples.
• The transverse magnetoresistance of a C₄CsBi_0.6 (stage 1, alpha-phase) sample at 1.2 K with a current of 1 mA. The current is applied in the graphite planes; the magnetic field is along the graphite c-axis.
• a) Fourier transform of the data in Figure . Most reproducible frequency is (1120 ± 110) T, although other frequencies sometimes occur. b) Comparison of the data from Figure with a simulated trace calculated using Equation 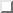and parameters obtained from the Fourier transform of the data. The calculated curve is offset from the data for clarity.
• (3root13 X 8)R(15°,0°) in-plane unit cell proposed for C₄CsBi_0.6 by A. Bendriss-Rerhrhaye.[17].
• a) Softening of the elastic constant C₃₃ as a function of composition in the C₈K_(1-x)Rb_x system. From Ref. [183]. The elastic constant was obtained from a fit to the acoustic branch of the phonon system. The phonons were observed using inelastic neutron scattering. Similar softening of the M-point optic modes has been seen using Raman scattering.[219] b) T_c versus x in the C₈K₍1-x)Rb_x system. Only the endpoint compounds have been characterized.
• Coherence lengths of a uniaxial superconductor. As pointed out by Morris et al.,[175] the coherence length of a uniaxial superconductor is the length of a vector from the center of a biaxial ellipsoid to its edge. a) The case of an aligned sample, which is described by Eqn. 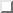. (See Figure a).) The ellipsoid has two radii of length xi_a and one of length epsilon xi_a. b) The case where the sample is tilted by an angle ø, which is described by Eqn. . Now the ellipsoid is triaxial, with one of the coherence lengths of size xi_a from a) being replaced by one of size xi_a sqrtcos² ø + epsilon² sin² ø.
• Cross-section of the flux quantum in a uniaxial superconductor. In all cases, the magnetic field is directed out of the paper. a) The aligned case. For vecH || ^c, the cross-section of the flux quantum along the field direction is circular. b) The tilted case. Now that the ellipsoid that determines xi(theta) is triaxial, the cross-section of the flux quantum is non-circular for all field orientations.