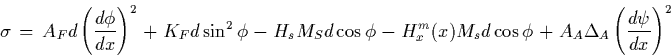
To explain the enhanced coercivity we propose the model that is a generalization of the model given in Ref. 11. Direct experimental observations of the magnetization reversal processes showed that the film remagnetization in the easy direction proceeds by domain wall nucleation and motion. Therefore, spin variations along the AF/FM interface need to be considered. We include these spin variations in equation 1 below (describing the energy density of the bilayer averaged over its thickness), which is simply an extension of eqn. 1 of Ref. 11:
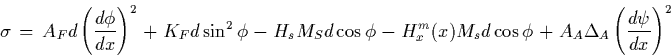
|
|
(1) |
where AF,
KF,
AA, and
KA are the
exchange and anisotropy constants of the FM and AF layers,
respectively, d is the FM thickness, ![]() is related to
the domain wall thickness in the AF layer,
Hx is the
external magnetic field, J is the AF/FM
interfacial exchange constant and
is related to
the domain wall thickness in the AF layer,
Hx is the
external magnetic field, J is the AF/FM
interfacial exchange constant and ![]() is the magnetostatic
field at the FM edge.
is the magnetostatic
field at the FM edge. ![]() and
and ![]() are respectively the directions of
the FM layer magnetization and AF layer spin vectors with
respect to the x axis (defined perpendicular
to the bilayer edge).
are respectively the directions of
the FM layer magnetization and AF layer spin vectors with
respect to the x axis (defined perpendicular
to the bilayer edge).
Near the interface, if ![]() one can assume that
one can assume that ![]() and
and ![]() change coherently. The coercivity is determined from the
stability criteria for non-uniform magnetization reversal
modes near the film edge. For the free FM layer this
yields[19]
change coherently. The coercivity is determined from the
stability criteria for non-uniform magnetization reversal
modes near the film edge. For the free FM layer this
yields[19]
|
|
(2) |
In a similar manner, for the AF/FM bilayer we have
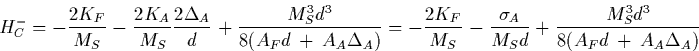
|
(3) |
|
|
(4) |
where
HC+
and
HC-
are the coercivities at the magnetic field orientations
parallel and antiparallel to the unidirectional anisotropy
axis, respectively, and ![]() . It follows that the
bilayer exchange anisotropy field and coercivity are
. It follows that the
bilayer exchange anisotropy field and coercivity are
|
|
(5) |
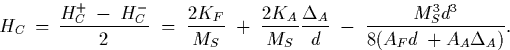
|
(6) |
So the exchange shift of the hysteresis loop
HE given by Eq.
(6) is the same as obtained in Ref. 11. In addition,
according to our model, the enhanced coercivity
HC appears as a
fundamental property of an AF/FM sandwich associated with
spin variations along the interface. The main point of our
treatment of the bilayer reversal is that we decomposed a
two-dimensional spin distribution of the AF into two
one-dimensional distributions: one parallel and one
perpendicular to the interface. The difference between
coercivities during remagnetization in opposite directions of
the bilayer [see equations (3) and (4)] occurs because in one
case it is necessary to overcome the energy of the spin
distribution in the AF both along and across the interface.
However, when a field of opposite polarity is applied there
is no necessity to overcome the energy of the spin
distribution perpendicular to the AF/FM interface. Moreover,
the energy stored in a planar domain wall compensates for the
energy cost of nucleating the spin homogeneity along the
interface. Therefore the term which is proportional to ![]() disappears from the
expression for
HC+
[compare Eqs. (3) and (4)]. In both cases we assume the
nucleation process at the edge of the sample is due to the
magnetostatic fields.
disappears from the
expression for
HC+
[compare Eqs. (3) and (4)]. In both cases we assume the
nucleation process at the edge of the sample is due to the
magnetostatic fields.
Clearly the asymmetry in the activity of the domain
nucleation centers observed cannot be explained by the above
model. To understand this asymmetry it is necessary to take
into account local variations of the antiferromagnetic
anisotropy. The physical origin for these variations is most
likely crystal lattice defects. In our bilayers, due to the
low magnetostriction of permalloy we neglect the anisotropy
variations due to stresses around crystal defects (like
dislocations) in the ferromagnet. Regions with enhanced
anisotropy in the antiferromagnet play no role when the
antiferromagnet does not have a Mauri-like[11] planar domain
wall, but they play a crucial role when there is such a
domain wall consisting of twisted spins in the NiO. The
energy associated with spin twisting is of order of ![]() . Therefore, spins at
places with enhanced
KA tend to
untwist at a lower magnetic field similar to the untwisting
of a torsional spring when the externally applied torque is
relaxed. This easier spin rotation in the antiferromagnet
results then in an easier local magnetization reversal in the
ferromagnet. Similar asymmetry in domain nucleation has been
observed earlier in the CoO/Co system.[2] We suggest that our
model can explain those observations as well, thereby
suggesting this phenomenon may be generic for all AF/FM
bilayers.
. Therefore, spins at
places with enhanced
KA tend to
untwist at a lower magnetic field similar to the untwisting
of a torsional spring when the externally applied torque is
relaxed. This easier spin rotation in the antiferromagnet
results then in an easier local magnetization reversal in the
ferromagnet. Similar asymmetry in domain nucleation has been
observed earlier in the CoO/Co system.[2] We suggest that our
model can explain those observations as well, thereby
suggesting this phenomenon may be generic for all AF/FM
bilayers.