Hc2(theta) in C4KHg

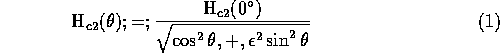
In Fig. 2, H_c2(theta) data are shown for two low-T_c C₄KHg samples, one a gold T_c = 0.95 K specimen prepared at MIT, and one a T_c = 0.73 K whose critical fields were reported by Iye and Tanuma.[50] The dotted lines are fits to the formula:

where epsilon is the critical field anisotropy parameter of Morris, Coleman and Bhandari[40] defined by:

epsilon = H_c2,par/H_c2,perp

and H_c2(0°) is . The fits were chosen to minimize the residual parameter :[6]

where the errors sigma_i are estimated as: sigma_i = 0.1 H^exp_i (1 + sin theta)

and nu is the number of free parameters. This form for the error is used to account for the fact that a small error in reading theta produces a much larger error in H_c2 when theta is near 90° than when theta is near 0°. Equation 1 describes the angular dependence of the critical field of anistropic 3D-coupled superconductors with uniaxial symmetry.[40,33] As Fig. 2 shows, this formula gives a good description of the H_c2(theta) data for low-T_c gold C₄KHg samples.

H_c2(theta) data for two T_c = 1.5 K samples is shown in Fig. 3 along with two curves produced by Eq. 1. The curve marked by () is the residual-minimizing curve according to the definition in Eq. 2. Using other reasonable definitions of the errors sigma_i in Eq. 2 (such as assuming an angle-independent error sigma_i = sigma) did not produce a fit that goes through the peak of the data. If the fit is forced through the data at theta = 90°, the solid curve in Fig. 3 is the result. Extensive experience in trying to fit the H_c2(theta) data of T_c = 1.5 K C₄KHg samples shows that Eq. 1 is simply inadequate as a detailed description of the experimental results.

There are several possibilities that come to mind as an explanation of the deviations from Eq. 1 that are displayed in Fig. 3. One possibility is that mosaic spread of the samples is affecting the data. The 2°-3° mosaic spread seen in neutron rocking curves can be accounted for by convolving Eq. 1 with a gaussian. This correction actually makes the agreement worse since the convolution broadens the H_c2(theta) peak. As the solid line in Fig. 3 shows, the fit that goes through the peak of the data is already much broader than the data.

Another possible extrinsic factor that could influence the angular dependence measurements is a possible misalignment of the sample during mounting. Detailed analysis of the consequences of improper mounting[10] demonstrates that the only effect of a tilted sample is to increase the measured value of . Because the H_c2(theta) curves are quite flat near theta = 0°, the effect of improper mounting for reasonable tilt angles (on the order of 5°) is negligible.

A more interesting explanation for the deviations seen in Fig. 3 is suggested by the specific heat data of Alexander et al. [4] Using the linear specific-heat coefficient = 0.95 mJ/(molK²) measured by Alexander, the zero-temperature thermodynamic critical field H_c can be estimated using the standard formula[55] . No superconducting transition was measured down to 0.8 K during the specific heat measurements,[4] so it is not clear that this linear specific heat coefficient is appropriate for a T_c =1.5 K sample. Nonetheless, an estimate of H_c can be made by assuming a (2 × 2)R0° structure. This procedure gives 112 gauss for H_c at T = 0 K. Using the usual quadratic form for the temperature dependence of H_c results in an estimate of 75 gauss for the thermodynamic critical field at a reduced temperature t == T/T_c = 0.57. Since, as Fig. 3 shows, 75 gauss is larger than the measured H_c2(theta) for theta less than about 70°, this value of H_c implies that superconductivity in T_c = 1.5 K C₄KHg samples is type I in character for most applied field orientations.

When H_c is greater than H_c2, H_c will be measured as the upper critical field. Since H_c is a thermodynamic quantity, it is expected to be angle-independent. If type I superconductivity is present for some range of angles, one therefore expects a modified angular dependence of the form

H_c2,eff(theta) = H_c2 where H_c2(theta) > H_c (type II region);
and H_c2,eff(theta) = H_c where H_c2(theta) < H_c (type I region). (3)

This type of angular dependence has previously been observed[37,56] in C₈K and in TaN. Using Eq. 1 for H_c2(theta), the modified form given by Eq. 3 has been fit to the angular dependence data for the T_c = 1.5 K C₄KHg samples. In the fits to Eq.3, H_c was taken as a free parameter in addition to H_c2(0°) and epsilon. The resulting fit is shown in Fig. 4. Consultation of standard tables on statistics[6] shows that the addition of the third free parameter H_c is justified by the factor of 1.5 reduction in the residual index. The hypothesis of type I superconductivity in the higher-T_c pink C₄KHg specimens therefore appears to be justified not only by the specific heat measurements of Alexander and coworkers,[4] but also by the improvement in the H_c2(theta) fits provided by the use of Eq. 3.